1102. Sticks problem
Xuanxuan has n sticks
of different lengths. One day, she arranged them in a row, with lengths s1, s2, s3,
..., sn. After measuring
each stick sk (1 ≤ k ≤ n), she noticed that for some pairs of sticks si
and sj (1 ≤ i < j ≤ n), the length of every stick placed between si and sj is strictly greater than si and strictly less than sj.
Given the sequence of lengths s1, s2,
s3, ..., sn, find the maximum possible
value of the difference j – i.
Input.
Consists of multiple test cases. Each test case consists of two lines. The
first line contains an integer n (n ≤ 50000) – the number
of sticks. The second line contains n distinct positive integers (not
exceeding 105) – the lengths of the sticks.
Output.
For each test case, print the maximum value of j – i on a separate line.
If no such indices i and j exist, print -1.
|
Sample input |
Sample output |
|
4 5 4 3 6 4 6 5 4 3 9 12 4 8 7 5 9
6 3 1 |
1 -1 4 |
SOLUTION
RMQ
+ binary search
Algorithm analysis
For each index i, find the maximum index k (i ≤ k ≤ n) such that RMinQ(si+1,
…, sk) > si. This can be done using binary search. Next, the desired index j is defined
as the position where the value RMaxQ(si,
…, sk) is attained for i ≤ j ≤ k.
Thus, for each index i, we need to find the
largest possible index j, and then, among all obtained pairs (i, j), determine the maximum difference j – i.
Example
Consider the third example.
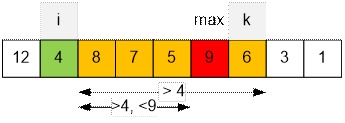
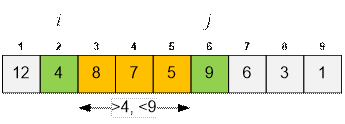
Let i = 2 (s2 = 4). The largest index k = 7 satisfies
the condition RMinQ(si+1,
…, sk) > 4. The value
of RMaxQ(s3, …, s7) is
attained at index j = 6.
Algorithm
implementation
Let’s declare the constants and arrays.
#define MAX 50010
#define LOGMAX 16
int dp_max[MAX][LOGMAX],
dp_min[MAX][LOGMAX];
int a[MAX];
The function Build_RMQ_Array builds RMQ tables for fast
minimum and maximum queries (dp_min and dp_max):
·
dp_min[i][j] stores the minimum value
over the segment of length 2j starting at position i.
·
dp_max[i][j] stores the index of the
element with the maximum value over the segment of length 2j starting
at i.
void Build_RMQ_Array(int *b)
{
int i, j;
for (i = 1; i <= n; i++)
{
dp_min[i][0] =
b[i];
dp_max[i][0] = i;
}
for (j = 1; 1 << j <= n; j++)
for (i = 1; i + (1 << j) - 1 <= n; i++)
{
if (b[dp_max[i][j - 1]] > b[dp_max[i + (1 <<
(j - 1))][j - 1]])
dp_max[i][j] =
dp_max[i][j - 1];
else
dp_max[i][j] =
dp_max[i + (1 << (j - 1))][j - 1];
dp_min[i][j] =
min(dp_min[i][j
- 1], dp_min[i + (1 << (j - 1))][j - 1]);
}
}
The RangeMaxQuery function returns the
index of the maximum element in the subsegment [i, j].
int RangeMaxQuery(int i, int j)
{
int k = 0;
while ((1 << (k + 1)) <= j - i + 1) k++;
if (a[dp_max[i][k]] > a[dp_max[j - (1<<k) +
1][k]])
return dp_max[i][k];
else
return dp_max[j - (1<<k) + 1][k];
}
The RangeMinQuery function returns the
minimum value in the subsegment [i, j].
int RangeMinQuery(int i, int j)
{
int k = 0;
while ((1 << (k + 1)) <= j - i + 1) k++;
return min(dp_min[i][k],dp_min[j - (1<<k) +
1][k]);
}
The BinSearch function uses binary search
on the interval [Left; Right] to find the largest index k such that all elements
between Left + 1 and k are greater
than a[Left].
int BinSearch(int
Left, int Right)
{
int MinValue = a[Left++];
if (RangeMinQuery(Left,Right) > MinValue) return Right;
while (Right > Left)
{
int Middle = (Left + Right) / 2;
if (RangeMinQuery(Left,Middle) > MinValue)
Left = Middle +
1;
else
Right = Middle;
}
if (dp_min[Left][0] <= MinValue) Left--;
return Left;
}
The main part
of the program. Process the
test cases sequentially.
while(scanf("%d",&n)
== 1)
{
for(i = 1; i
<= n; i++) scanf("%d",&a[i]);
Build the RMinQ and RMaxQ arrays.
Build_RMQ_Array(a);
For
each index i:
·
Using
BinSearch(i, n), find the largest index k
such that all elements in the interval [i +
1; k] are greater
than a[i];
·
In
the interval [i, k] find the index j where the maximum
value is reached.
·
Check whether j – i is the largest difference.
res = 0;
for(i = 1; i <= n; i++)
{
k = BinSearch(i, n);
j =
RangeMaxQuery(i,k);
if (j - i > res) res = j - i;
}
Print the result. If res = 0, we should print -1.
if (res == 0) res = -1;
printf("%d\n",res);
}